Binary Search Tree

This article is the continuation of a series of articles on algorithms and data structures. The previous one was about quicksort.

Why a binary search tree (BST)?

If you remember from the previous article on quicksort, the only reason why we were sorting our words in the first place is because we decided to solve the problem using a dynamic array.

Our new assumption is that we actually don’t need the words in order in an array. We just need to implement the concept of a Set! A set, just like in the mathematical sense, it’s a data structure that supports the contains operation and doesn’t have duplicates.

Implementing a Set with a BST

We go back again to the concept of Node that we had before with the linked list but this time we don’t have just one reference to the next element, we actually have two references: the left node and the right node.

For the linked list we had this:

class Node<T>(val data: T, var next: Node<T>?)

Now we need to have this:

class Node<T>(
  val data: T, 
  var left: Node<T>?, 
  var right: Node<T>?
)

A graphical representation of a binary search tree is like this:

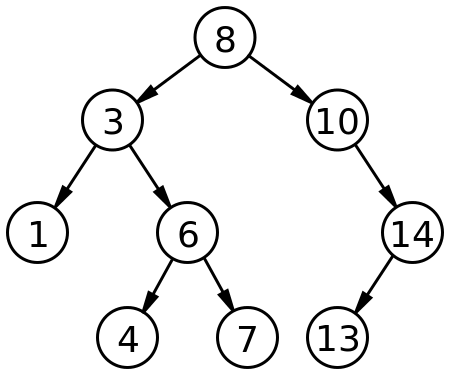
We want to have a class called Set that has the add and contains operations.

The add operation

To add an element to the BST we need to check to which direction we want to insert the new node. If the new element is lower than the root we insert to the left. If it’s bigger we insert to the right. If it’s the same element we ignore it because the set doesn’t have duplicates by definition.

class Set<E : Comparable<E>> {
  private var root: Node<E>? = null

  fun add(element: E) {
        root = add(element, root)
  }

  private fun add(e: E, node: Node<E>?): Node<E> {
    when {
      node == null -> return Node(e)
      e < node.data -> node.left = add(e, node.left)
      e > node.data -> node.right = add(e, node.right)
    }
    return node as Node<E>
  }

  // ...
}

The contains operation

For the contains operation we have to do the same. If the root has the element we want, we found it. If it doesn’t we search to the left or to the right depending on the element being smaller or larger than the root.

fun contains(element: E): Boolean = contains(element, root)

private fun contains(e: E, node: Node<E>?): Boolean {
  when {
    node == null -> return false
    e == node.data -> return true
    e < node.data -> return contains(e, node.left)
    e > node.data -> return contains(e, node.right)
    else -> return false // can't happen
  }
}

Performance

Even though we assumed that using a BST would be a better solution it turns out that it’s not. It takes 806ms to load all the words and 5ms to find the permutations.

Even worse, if we try to load the original dictionary file where the words are almost all sorted, it crashes with a StackOverflowError.

Why is it slower?

The problem with a binary search tree is that it only works if the elements are mostly randomly ordered. If we happen to be unlucky enough to have the input file already sorted, we will always add to the right side of the root and we will effectively end up with a linked list and not a tree and we saw already that a dynamic array performs better than a linked list.

How to improve the performance?

A way to improve the performance of the binary search tree was first introduced in 1962 called AVL tree named after their creators Adelson-Velsky and Landis.

It’s a self-balancing binary search tree, which means that you never have too many nodes on the left or too many on the right.

We will look into this improvement in a future article. Stay tuned!